Introduction
- arrow_drop_down_circle
Présentation
Les pentominos sont les différentes formes composées en assemblant 5 carrés. Il existe 12 combinaisons possibles. Or comme par magie ces pentominos peuvent s'assembler pour former différents rectangles de 60 cases (5 carrés x 12 pentominos). Les tailles des rectangles peuvent être 6x10, 5x12, 4x15 et 3x20. Il est également possible d'assembler les 12 pentominos dans un carré 8x8 en choisissant de laisser 4 cases vides. Les pentominos peuvent être également composées en assemblant 5 cubes. On peut alors également remplir les parallélépipèdes de taille 3x4x5, r2x5x6 et 2x3x10.
Découvrir iPento l'interface graphique qui vous permet de jouer aux pentominos.
- arrow_drop_down_circle
Le concept des "polyominos"
Les pentominos font parties des polyominos, notion principalement inventée et décrite par le mathématicien Solomon W. Golomb dans son livre intitulé "Polyominoes" paru au début des années soixante et qui constitue la référence sur le sujet. (en vente sur amazon.com).
Les polyominos composés de deux carrés sont les dominos.
Le puzzle des pentominos
- arrow_drop_down_circle
Les 12 pentominos
Par analogie de forme, une lettre est affectée à chacun des 12 pentominos.
F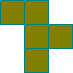 I
I L
L N
N P
P T
T U
U V
V W
W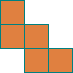 X
X Y
Y Z
Z
- arrow_drop_down_circle
Les solutions
Nombre de solutions en fonction du rectangle :
- Rectangle 6 x 10 : 2339
- Rectangle 5 x 12 : 1010
- Rectangle 4 x 15 : 368
- Rectangle 3 x 20 : 2

- arrow_drop_down_circle
Les solutions en 3 dimensions
- Parallélépipède 3 x 4 x 5 : 3940
- Parallélépipède 2 x 5 x 6 : 264
- Parallélépipède 2 x 3 x 10 : 12
- arrow_drop_down_circle
Liens
fr.wikipedia.org : La page wikipédia Pentomino
www.xs4all.nl/~gp/PolyominoSolver/Polyomino.html : solutions
www.recmath.org/PolyPages : The Poly Pages : site très complet sur les poly-ominoes, poly-cubes etc...
villemin.gerard.free.fr : Site Diconombre